Axial Flux Motors

1. Fundamental Magnetic Flux Orientation

graph LR
    subgraph "Radial Flux Motor"
        A[Stator] --> B[Air Gap]
        B --> C[Rotor]
        D[Flux Direction: ⟂ to shaft]
    end
    
    subgraph "Axial Flux Motor"
        E[Stator Disc] --> F[Air Gap]
        F --> G[Rotor Disc]
        H[Flux Direction: ∥ to shaft]
    end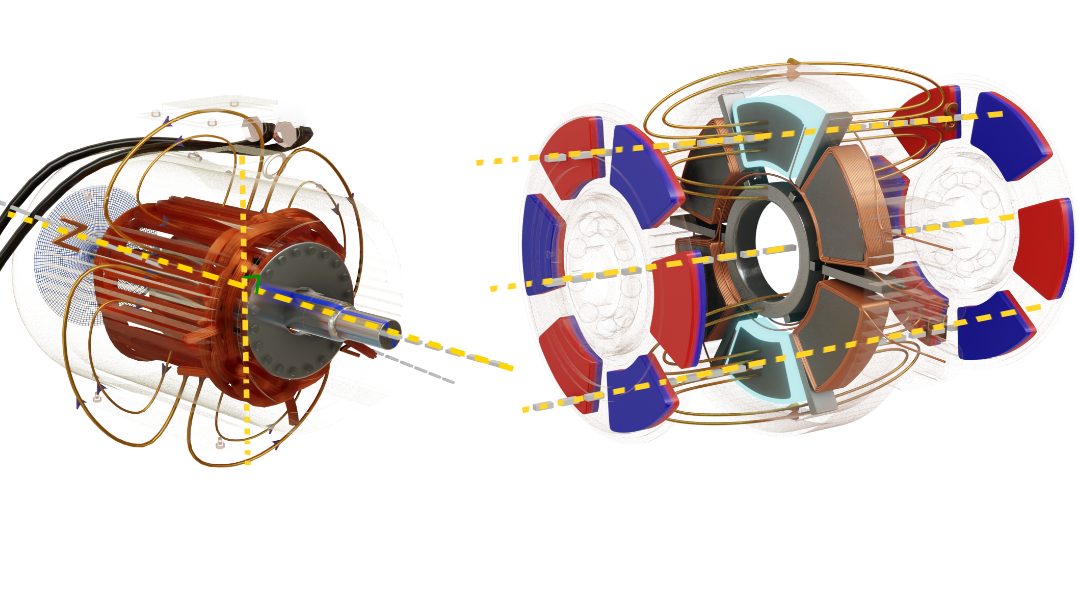

Radial Flux Motors (Traditional)

Flux Direction: Magnetic flux flows radially from rotor to stator (perpendicular to shaft axis)
Air Gap: Cylindrical air gap between rotor and stator
Magnetic Circuit: Flux crosses the air gap in the radial direction
Field Distribution: Magnetic field lines are perpendicular to the axis of rotation

Axial Flux Motors

Flux Direction: Magnetic flux flows axially along the shaft direction (parallel to shaft axis)
Air Gap: Flat, disc-shaped air gap(s) parallel to rotor face
Magnetic Circuit: Flux crosses the air gap in the axial direction
Field Distribution: Magnetic field lines are parallel to the axis of rotation

2. Construction Architecture

graph TD
    subgraph "Radial Flux Construction"
        A1[Cylindrical Stator] --> A2[Slotted Core]
        A2 --> A3[Distributed Windings]
        A4[Inner Rotor] --> A5[Magnets/Windings]
        A5 --> A6[Cylindrical Air Gap]
    end

graph TD
    subgraph "Axial Flux Construction"
        B1[Disc Stator] --> B2[Concentrated Windings]
        B3[Disc Rotor] --> B4[Surface Magnets]
        B4 --> B5[Flat Air Gap]
        B6[L/D Ratio less than 0.3]
    end

Radial Flux Design

Traditional cylindrical construction:

Stator: Cylindrical with slots for windings
Rotor: Inner cylinder with magnets/windings
Length/Diameter Ratio: Typically $\frac{L}{D} > 0.5$
Cooling: Radial heat dissipation paths

Axial Flux Design

Disc-like construction:

Stator: Flat disc with concentrated windings
Rotor: Disc with surface-mounted magnets
Length/Diameter Ratio: Very low $\frac{L}{D} < 0.3$
Cooling: Axial heat dissipation through large surfaces

3. Electromagnetic Theory Differences

graph LR
    subgraph "Torque Generation"
        A[Magnetic Field B] --> C[Force on Conductor]
        B[Current I] --> C
        C --> D[Torque = r × F]
    end
    
    subgraph "Scaling Laws"
        E[Radial: T ∝ D²L] 
        F[Axial: T ∝ D³]
    end

Torque Production

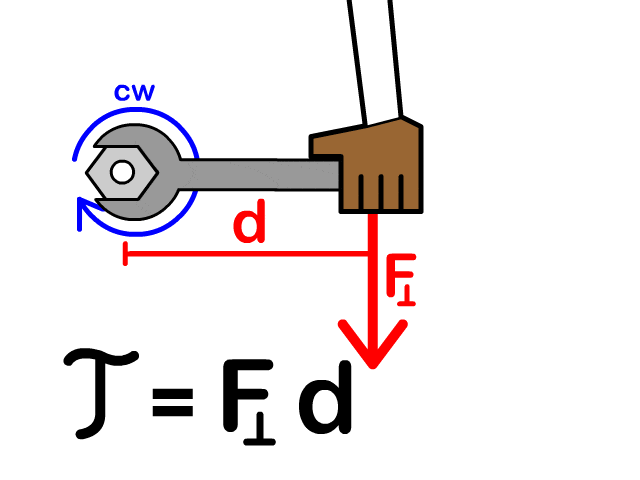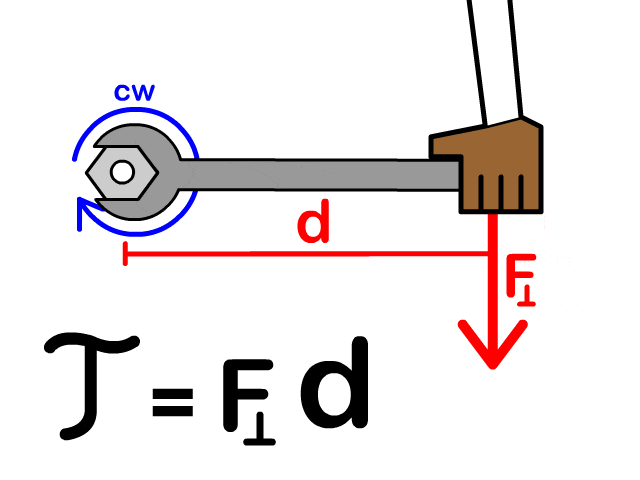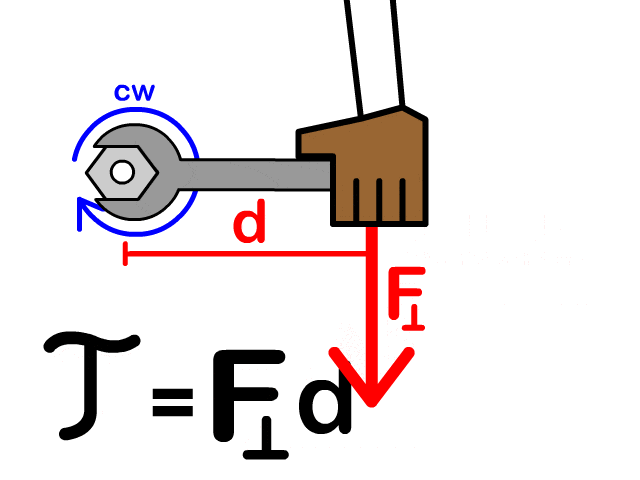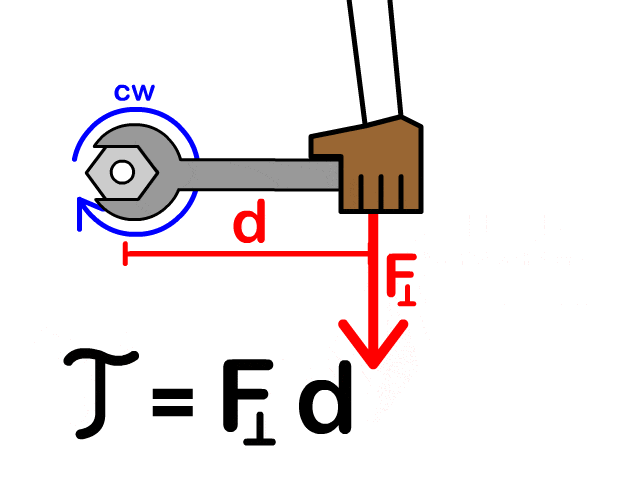
Radial Flux:

T = k \times B_{radial} \times I \times L_{active}

Active length is axial dimension
Torque density limited by radial magnetic loading

Axial Flux:

T = k \times B_{axial} \times I \times r_{active}^{2}

Active area scales with radius squared
Higher torque density potential at larger diameters

EMF Generation

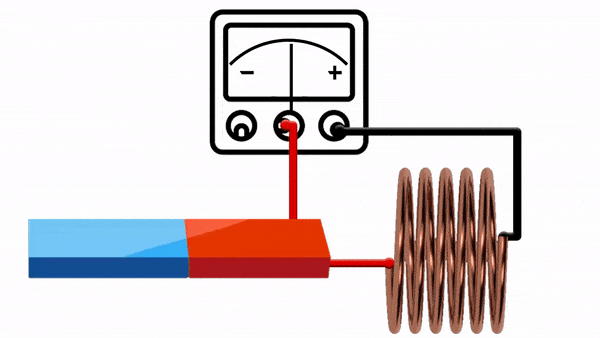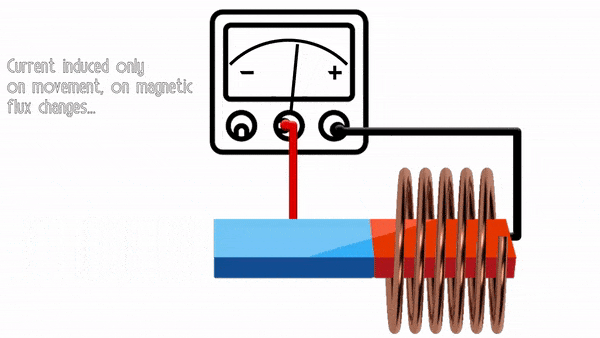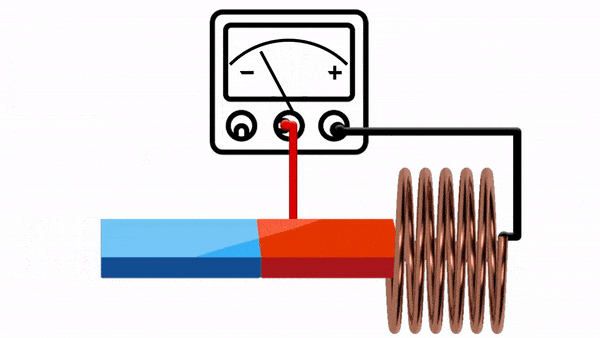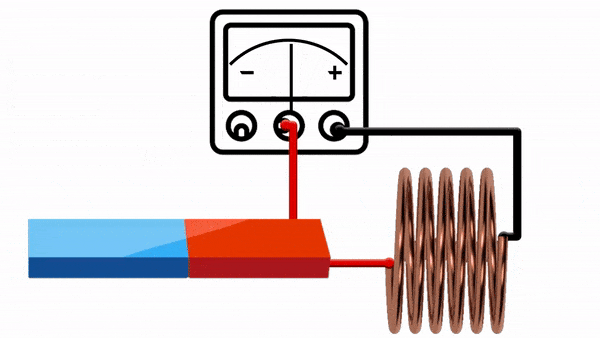
Radial Flux:

EMF = B \times l \times v

where $l$ = axial length

Flux linkage through cylindrical surface

Axial Flux:

EMF = B \times r \times ω \times N

where $r$ = radius

Flux linkage through disc surface
Higher EMF at larger radii due to increased velocity: $v = r ω$

4. Magnetic Circuit Analysis

graph TD
    subgraph "Radial Flux Path"
        A1[N Pole] --> A2[Air Gap] 
        A2 --> A3[Stator Tooth]
        A3 --> A4[Stator Back Iron]
        A4 --> A5[Return Path]
        A5 --> A6[S Pole]
    end
    
    subgraph "Axial Flux Path"
        B1[N Pole] --> B2[Axial Air Gap]
        B2 --> B3[Stator Core]
        B3 --> B4[Radial Return]
        B4 --> B5[S Pole]
    end

Reluctance Considerations

Radial Flux:

R = \frac{l}{μ_{0} μ_{r} A}

where $l$ is radial distance

Magnetic path through cylindrical iron core
Flux density uniform across air gap height

Axial Flux:

R (r) = \frac{g}{μ_{0} A (r)}

where $A (r) = 2 π r \cdot w$

Magnetic path through disc-shaped iron core
Variable reluctance with radius
Non-uniform flux density (higher at inner radius)

Leakage Flux

Radial Flux:

End-turn leakage at motor ends
Slot leakage between conductors
Predictable leakage patterns

Axial Flux:

Edge effects at disc periphery
Inter-disc leakage in double-sided designs
3D magnetic field effects more significant

5. Power Density & Scaling Laws

graph LR
    subgraph "Scaling Relationships"
        A[Radial: P ∝ D²L] --> C[Linear Volume]
        B[Axial: P ∝ D³] --> D[Cubic Diameter]
        end

graph TD 
subgraph "Heat & Surface Area"    
        E[Heat ∝ Surface Area] --> F[Radial: ∝ DL]
        E --> G[Axial: ∝ D²]
    end

Radial Flux Scaling

P \propto D^{2} \times L

where $D$ = diameter, $L$ = length

Limited by aspect ratio constraints
Heat dissipation through cylindrical surface $\propto D \times L$

Axial Flux Scaling

P \propto D^{3}

Superior scaling for larger diameters
Heat dissipation through flat surfaces $\propto D^{2}$
Better power-to-weight ratio for large diameters

Power Density Comparison:

\frac{P}{V} = \frac{P}{\frac{π D^{2} L}{4}} (Radial) vs \frac{P}{V} = \frac{P}{\frac{π D^{2} t}{4}} (Axial)

where $t$ = axial thickness

6. Winding Configurations

flowchart TD
    A[Radial Windings] --> B[Long End Turns]
    C[Axial Windings] --> D[Short End Turns]
    B --> E[Higher Resistance]
    D --> F[Lower Resistance]

Radial Flux

Distributed windings: Conductors spread across multiple slots
Concentrated windings: Each coil around single tooth
Resistance: $R = ρ \frac{l}{A}$ where $l$ includes long end turns
Standard 3-phase winding arrangements

Axial Flux

Toroidal windings: Around disc core (less common)
Concentrated non-overlapping: Each coil encircles single tooth
PCB windings: Flat spiral conductors
Resistance: Lower due to shorter end turns: $l_{end} \approx \frac{π D}{6 p}$

7. Performance Characteristics

graph TD
    A[Losses] --> B[Copper I²R]
    A --> C[Iron Core]
    A --> D[Mechanical]

graph LR    
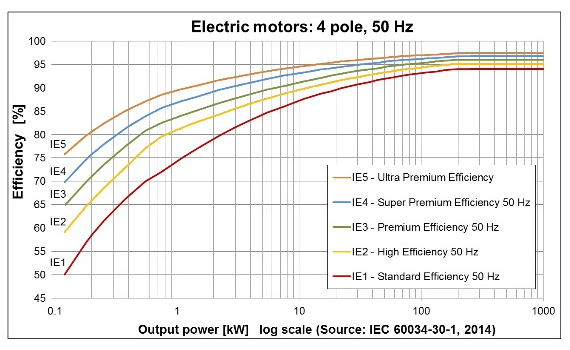
    E[Efficiency] --> F[Pout/Pin]

Efficiency Comparison

General Efficiency Formula:

η = \frac{P_{out}}{P_{out} + P_{losses}} = \frac{P_{out}}{P_{in}}

Radial Flux:

Mature technology with optimized designs
Well-understood losses and mitigation
Efficiency: $η = 85 % - 96 %$ depending on size/design

Axial Flux:

Potentially higher efficiency due to:
- Shorter end turns: $R_{axial} = 0.85 \times R_{radial}$
- Better heat dissipation: $Δ T \propto \frac{P_{loss}}{A_{surface}}$
- Optimized magnetic circuit
Efficiency: $η = 90 % - 98 %$ in well-designed systems

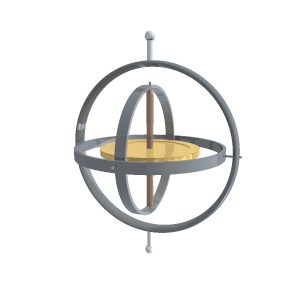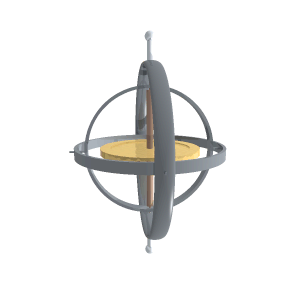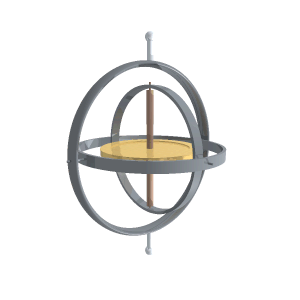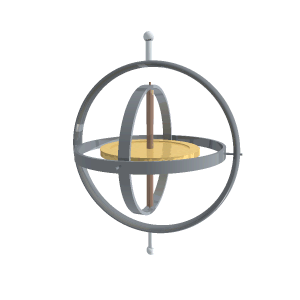
Speed Capabilities

Mechanical Speed Limit:

n_{max} = \sqrt{\frac{σ_{max}}{ρ π^{2}}} \times 60

where $σ_{max}$ = material stress limit, $ρ$ = density

Radial Flux:

Standard bearings and mounting
Rotor dynamics well understood

Axial Flux:

Lower rotational inertia: $I = \frac{1}{2} m r^{2}$ (disc) vs $I = \frac{1}{2} m (r_{1}^{2} + r_{2}^{2})$ (cylinder)
Axial magnetic forces: $F_{z} = \frac{B^{2} A}{2 μ_{0}}$
Potential for higher acceleration: $α = \frac{T}{I}$

8. Design Trade-offs

graph LR
        A[Cost] --> A1[Radial: Lower]
        A --> A2[Axial: Higher]

graph LR        
        B[Power Density] --> B1[Radial: Good]
        B --> B2[Axial: Excellent]

graph LR         
        C[Manufacturing] --> C1[Radial: Mature]
        C --> C2[Axial: Complex]

graph LR         
        D[Cooling] --> D1[Radial: Limited]
        D --> D2[Axial: Superior]

Advantages & Disadvantages

Aspect	Radial Flux	Axial Flux
Manufacturing	Mature, standardized	Complex, specialized tooling
Cost	Lower (volume production)	Higher (specialized)
Power Density	Good for small-medium sizes	Excellent for large diameters
Cooling	Limited surface area	Large flat surfaces
Bearing Loads	Radial forces only	Axial + radial forces
Scalability	Linear with volume	Cubic with diameter

Cost Analysis:

T C O = P u r c h a s e P r i c e + \frac{A n n u a l E n e r g y C o s t}{D i s c o u n t R a t e}

9. Applications & Selection Criteria

flowchart TD
    A[Motor Selection] --> B{Application?}
    B -->|Standard| C[Radial]
    B -->|Space Limited| D[Axial]
    B -->|Cost Critical| C
    B -->|High Power| D

Choose Radial Flux When:

Standard industrial applications
Cost is primary concern: $\frac{Cost}{kW} < threshold$
Proven reliability required
Small to medium power ratings ( $P < 100 kW$ )
Established supply chains needed

Choose Axial Flux When:

Space constraints (pancake form factor): $\frac{L}{D} < 0.5$
High power density required: $\frac{P}{V} > threshold$
Direct drive applications: $n_{motor} = n_{load}$
Wheel hub motors: $T = F \times r_{wheel}$
Large diameter, low speed: $D > 500 mm$ , $n < 1000 RPM$

Selection Formula:

Merit Factor = \frac{η \times P_{density}}{Cost \times Complexity}

10. Future Developments

timeline
    title Motor Technology Evolution
    
    2020 : Traditional Radial Flux
         : Silicon Steel Cores
         : Ferrite Magnets
    
    2025 : Advanced Materials
         : Amorphous Steel
         : Rare Earth Magnets
         : Better Thermal Management
    
    2030 : Manufacturing Revolution
         : 3D Printed Components
         : Automated Winding
         : Cost Reduction
    
    2035 : Next Generation
         : AI-Optimized Designs
         : Novel Cooling Systems
         : Modular Architecture

Radial Flux Evolution

Advanced materials (rare earth magnets, amorphous steel)
Improved manufacturing techniques
Better thermal management: $q = h A Δ T$
Higher speed capabilities

Axial Flux Innovation

Manufacturing cost reduction
3D printed components
Advanced magnetic materials: $B_{rem} > 1.4 T$
Integrated thermal management
Modular designs for scalability

Technology Readiness Levels:

TRL = f (Research, Development, Demonstration, Deployment)

PCB Motor Adaptation of Axial Flux Design

PCB motors represent the ultimate evolution of axial flux motor technology, leveraging printed circuit board manufacturing to create ultra-flat, highly efficient motors.
The inherent disc geometry of axial flux motors translates perfectly to PCB construction, where copper windings are etched directly onto flat substrates rather than wound with traditional wire.
Key Adaptations:
Flat spiral windings replace bulky 3D coils, eliminating end turns entirely
Multi-layer PCB stacks create concentrated magnetic fields in minimal axial space
Precise manufacturing tolerances from PCB fabrication enable tighter air gaps
Integrated cooling through copper pours and thermal vias in the PCB substrate
References

Click here to Learn about Axial Motor Calculations